Introduction to Algebraic Curves, 201.2.4451, (2018, Spring).

The prerequisites for the course are (solid knowledge of): Calculus 3, Algebraic Structures.
Some knowledge of Complex Functions is not a prerequisite at the beginning, but will be needed by the middle of semester.

The classes are on Tuesdays, 10:10-12:00, ([58], -101) and Wednesdays, 10:10-12:00 ([58], -101)
There will be no lectures during the first week of the semester. The first lecture will be on 13.03.
As the catch up, we will have additional hour(s) on Wednesdays, 14:10-15:00, ([58], -101)

Homeworks: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14,


       

The ancient study of circles/parabolas/hyperbolas has evolved through centuries to the rich theory of algebraic curves (and Riemann Surfaces). Today this well-developed topic involves variety of methods from algebra, analysis, geometry and topology. Our course will be a modest introduction to this topic. The course can serve as the preparation/motivation for the solid courses in Algebraic Geometry, Commutative Algebra.

Our progress:
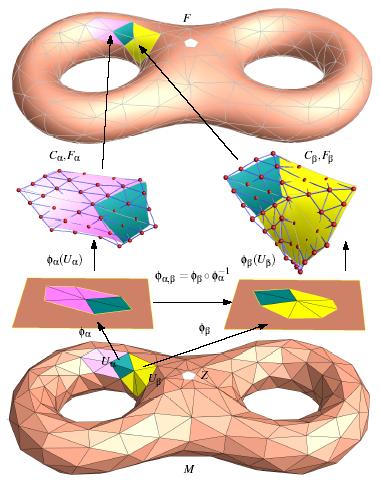
(weeks 2&3) Definition of real/complex manifolds. Riemann surfaces, basic examples.
(week 4) Basic properties of holomorphic maps of Riemann surfaces. The degree of the map.
(week 5) The degree of the map. Topological Structure of R.S. Hurwitz formula. Plugging punctures in Riemann Surfaces.
(week 6, 2 hours) Complex tori.
(week 7, 5 hours) Algebraic sets. Hilbert basis theorem. Hilbert Nullstellensatz.
(week 8, 5 hours) Local rings and localization. DVR. Local properties of plane curves.
(week 9, 4 hours) The local intersection multiplicity. Algebraic sets in P^n.
(week 10, 4 hours) Algebraic sets in P^n. Algebraic curves in P^2. Bezout theorem.
(week 11, 4 hours) Group law on plane cubic. Noether's AF+BG. Linear Sytems of curves. Zariski topology.
(week 12, 2 hours) Algebraic Varieties. Their rings of regular/rational functions. Morphisms.
(week 13, 2.5 hours) The field of rational functions. Dimension of variety. Birational equivalence of varieties.
(week 14, 4.5 hours) Rational maps of curves. Singularities and desingularization. Divisors. Riemann theorem.
(week 14, 4.5 hours) Genus of plane algebraic curves. Differentials and derivations. Riemann-Roch theorem.

Textbooks:
W.Fulton "Algebraic Curves. An introduction to algebraic Geometry".
R.Miranda "Algebraic Curves and Riemann Surfaces".